Grayscale and color image enhancement

I've put a few operations here that are relatively simple and in wide use for improving the appearance of grayscale and color images. Each one will be described below. The first two, gamma correction and contrast enhancement are trivial to implement because they only require a lookup table to map from the source pixel value to the dest pixel value. The last two, unsharp masking and image smoothing are a little more complicated because they use some set of neighboring pixels in the source to determine the dest pixel value. All four operations work separately on each color sample, so the color implementation for each one just uses its grayscale implementation three times (once for each color sample). There are many other image processing operations that can be included here, and they will be added as occasion permits. If you have a favorite that's not here, ask me.

What other types of enhancement operations exist?

Image restoration takes an image that has been degraded by some known (typically statistical) process and attempts to regenerate something closer to the original image. These methods are often Bayesian, selecting destination pixels using a maximum a posteriori procedure. The basic idea is very simple. You have a statistical model for the degradation process, given as a set of conditional probabilities for observing a specific degraded pixel when you started with some original pixel. You also have an estimate of the prior probabilities for the original image pixels (or groups of them). Bayes law then lets you estimate the posterior conditional probabilities, which are the probabilities that, given an observed (degraded) pixel, you started with some original one; and you select the maximum of these over the set of all possible original ones. By doing this, you select the original image pixel that is most likely to have produced the observed pixel.

If the noise is known to be sparse additive gaussian ("sparse" meaning that only a small fraction of the pixels are affected), an obvious operation to apply is a median filter, which is very good at removing outliers without seriously affecting other pixels. It is nonlinear, has some smoothing effect, and tends to change pixels at sharp edges.

For binary images, enhancement involves a number of operations, such as removal of pepper noise. If the image has been scanned, cleanup can involve deskew, removal of black pixels near the edge, and special operations on binarized pictorial regions. The latter can involve conversion to gray, followed by grayscale enhancement and halftone screening back to binary. Many scanners give you binary output, and if they threshold the pictorial regions without halftoning or dithering, the result is a high contrast image where much of the gray information can be lost.

But things get much more complicated with flat panel displays. Whereas CRTs emit light from the phosphor that is proportional to the electron current hitting it, flat displays use a white illumination with light subtraction due to absorption in the dyes. Flat panels do not have a built-in physical gamma to darken the image; consequently, images look much brighter than on CRTs.

There is also a calibration for displays that has to do with the relative amount of different colors used to produce white. This is expressed by the temperature of the black body radiator that would produce this color distribution. The standard is 6500 degrees K, but manufacturers have found that if they use higher equivalent temperatures, the displays are brighter, and the extra blue is not too noticeable because the eye is relatively insensitive to blue. So, for example, an inexpensive CRT may be calibrated to 12000 degrees K.

What about printing? If you print from a digital camera image without using a gamma correction, the image will appear light and washed out. So printing software typically compensates for the high gamma of the camera.

From a psychophysical viewpoint, people experience intensity logarithmically. Each doubling of the intensity is perceived as an additive constant to the apparent brightness. Our eyes have a dynamic range of about 10⁶, whereas your camera has a mere 8 bits (256 levels) in each color. If the camera were linear, a scene with both light and shadowed regions could have both the shadowed region too dark and the light region washed out. The positive gamma built in to cameras helps somewhat in this respect. The apparent dynamic range in the dark parts of the image is increased, because more of the actual range is assigned to these darker pixels. This gives the camera a logarithmic response. Of course, the lighter part gets even lighter, but not by as much.

So gamma mapping is used both to compensate for nonlinearities in the display devices and to increase the apparent dynamic range. The output is related to the input by raising it to the factor (1 / gamma), properly scaled so that the end points are not adjusted. The mapping function looks like this:

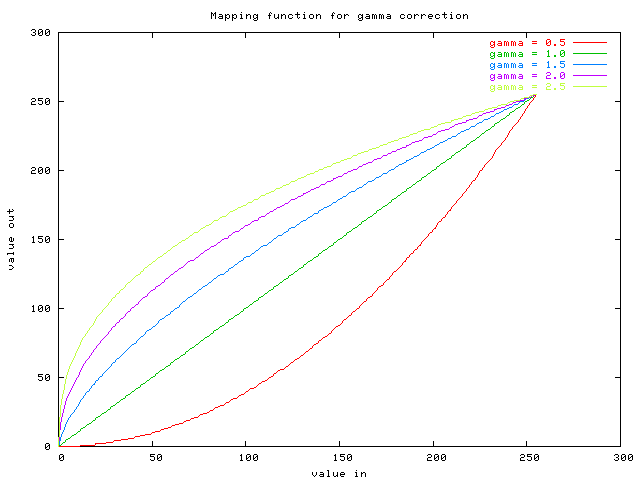
The plot was made using prog/gammatest.c. If gamma < 1.0, the image is darkened, with the biggest effect happening for the dark (low input) pixel values. If gamma > 1.0, the image is brightened overall, with the largest changes happening again for the dark shadows.

We provide a top-level interface pixGammaCorrect() in enhance.c. For display on a CRT, depending on the source of the image, you may want to apply a gamma in the range 1.5 to 2.0. For printing, again depending on the image source, you may want to apply a gamma that is less than 1.0 to darken the image.

How does one generate a sigmoid curve? One obvious way is to integrate under a gaussian; this gives a set of curves with a single parameter. Unfortunately, such an integral is not an elementary function, so you'd have to use a table. As an alternative, consider integrating under a lorentzian. The lorentzian goes as 1/(a² + x²), and consequently has large tails compared to the gaussian. But the lorentzian integrates simply to the arctan function. This makes a transition between -pi/2 and +pi/2 as the angle goes from large negative to large positive values. Using a single parameter to scale the angle, the result is to take a slice of the function centered about 0. The parameter is just the width of the slice, in appropriate units. As the parameter approaches 0, the width gets small, so we're using the arctan function near 0, which is linear and hence sets the output equal to the input. As the parameter increases, the contrast increases. The output is scaled and translated so that the min and max values of input and output coincide (here, at 0 and 255). The mapping function looks like this:

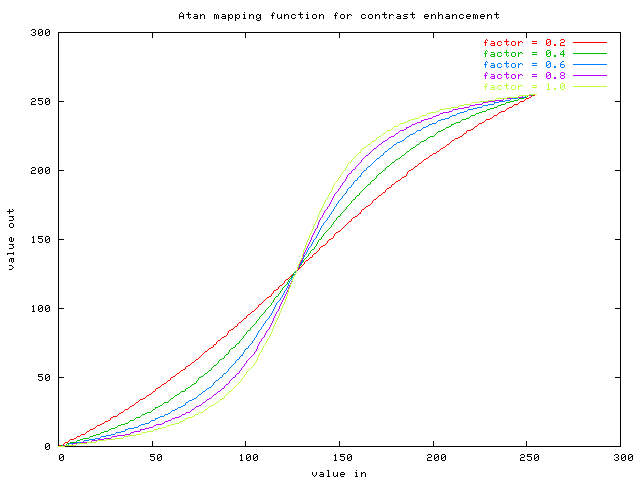
The plot was made using prog/contrasttest.c. See that file or the implementation in pixEnhanceContrastGray() for details. Values of the input parameter greater than 0.0 increase the contrast. (Values less than 0.0 should decrease it; this is not implemented, however.) The top level interface, which takes both 8 bpp grayscale and full color images, is pixEnhanceContrast() in enhance.c.

The method implemented here is called unsharp masking. The high pass "edge" image is generated by convolving the image with an approximation to a laplacian filter. In such a filter, the center has a value 1.0 and some set of N surrounding pixels each has a value -1.0/N. For a 3x3 filter, this would look like

    -1/8   -1/8   -1/8
    -1/8     1    -1/8
    -1/8   -1/8   -1/8

     1/9    1/9    1/9
     1/9    1/9    1/9
     1/9    1/9    1/9

    -1/9   -1/9   -1/9
    -1/9    8/9   -1/9
    -1/9   -1/9   -1/9

Once the edge image has been generated, some fraction of it is added to the original image. Thus, there are two parameters:

1. The size of the smoothing filter, given by 2s + 1. For s = 0, the filter has unit size (support), and hence it is the identity. The edge image is then 0, so there is no edge sharpening. The 3x3 filters given above are used to generate the edge image when s = 1.
2. The fraction f of the edge image added back. Typical useful values of f range between 0.2 and 0.7.